puzzles 1

Comment les puzzles de Tatham m'ont aidé à écrire ma thèse

J'ai toujours aimé les puzzles, les trucs qui sont dans le désordre et qu'il faut ordonner, ou les trucs qu'il faut compléter, équilibrer, distribuer, etc. Puzzles, ici, c'est au sens large, ça comprend aussi bien les casse-têtes et autres rubik's cubes, que le tricot et les tableaux pré-peints que l'on remplit avec du fil de coton ou de la laine, que les mots-fléchés et les sudokus dans les magazines, que les énigmes et autres exercices à solution dans des livres dédiés (comme ceux du logicien R. Smullyan ). Je n'arrive pas toujours à les terminer, mais ce n'est pas important.

Un puzzle se pratique...

Par exemple, les sudokus de niveau 13 et 14 me laissent absolument pantois et je n'ai jamais cherché à comprendre comment les résoudre, j'ai bien assez de choses compliquées à faire par ailleurs. Ce que j'aime dans les puzzles, c'est que l'objectif c'est de les terminer. S'il y a sans aucun doute une satisfaction propre à cela, qui peut motiver à leur étude, toutefois c'est un processus complètement différent d'un score ou d'un classement qui donneraient envie d'être le ou la plus fort·e, d'être "prem's". Les puzzles sont un espace de pratique avant tout, avec l'idée que la pratique transforme les pratiquant·es.

D'ailleurs, pour moi, deux choses sont importantes dans l'appréhension des puzzles en général. La première, c'est que, souvent, la fin d'un puzzle est moins satisfaisante que le passage d'une portion précédente. La fin, on la voit venir, on a déjà compris l'essentiel, tout est comme déjà dans l'ordre, il n'y a plus qu'à effectuer les gestes ("les épis sont bien rangés", dirait le dernier poème du yiking, H64). Par contre, quand on trouve le puzzle à son niveau, quel que soit ce niveau, on est face à une difficulté inédite, on doit sortir de ses habitudes, on doit reconsidérer ses propres perspectives, et on doit admettre qu'on était peut-être pas encore assez outillé·e pour réussir. Et justement, il faut bien en passer par là pour avancer.

La seconde caractéristique d'un puzzle, c'est que, restant une expérience individuelle, les puzzles ne donnent pas envie de tricher. Lire le mode d'emploi avant d'avoir essayer de trouver, ou remplir des cases de chiffres ou de lettres sans savoir pourquoi n'aurait aucun sens, sinon de se mentir à soi-même. Déjà, la plupart ne le permettent matériellement pas. Ensuite, même si l'on dispose de solutions accessibles, sauter une étape du puzzle n'apporte rien de plus que de l'abandonner. Il m'arrive de regarder régulièrement les solutions de certaines grilles, pas pour découvrir quelque chose que je ne saurais trouver par moi-même, mais pour vérifier que mon raisonnement me mène au bon résultat, notamment quand mon stylo ne s'efface pas. Si le résultat n'est pas celui que j'attendais, je reprend mon parcours en amont au lieu de remplir la case, et je me fais un plaisir de ne pas la remplir tant que je n'ai pas trouvé le raisonnement adéquat.

Parce que ce qui compte, au final, c'est de parcourir le puzzle, de suivre la logique particulière qu'il se propose de nous faire découvrir. Les puzzles sont avant tout un espace de pratiques méditative, récréative, relaxante, focalisante, bref, ils font travailler l'esprit et lui permettent de découvrir certains mécanismes logiques et cognitifs, sans forcément constituer un travail en eux-mêmes. Il y a des puzzles que l'on réalise une seule fois, il y a des puzzles sur lesquels on revient (on réapprend à terminer un rubik's cube tous les 10ans par exemple), il y a des puzzles que l'on fait presque tous les jours...

Hexagone, tatata...

Parmi les puzzles que j'aime bien, ceux avec des grilles fondées sur un motif hexagonal plutôt que orthogonal me plaisent souvent beaucoup plus que les autres. Je n'ai pas d'explication à cette préférence, ça déstabilise un peu par rapport au quadrillage orthogonal de bien des jeux, c'est plus ludique. Le puzzle déguisé en jeu vidéo HexaHop a ainsi occupé les nuits de mes premiers mois de rédaction, dans l'hiver Bruxellois. Un personnage parcours des séries de motif hexagonaux et doit détruire l'ensemble du motif pour compléter le niveau, et parfois y ajouter un objectif déterminé. Un autre type de grille hexagonale est plus courant, qu'il serve à accomplir des mots-croisés ou bien qu'il relève plutôt de la famille des sudokus.

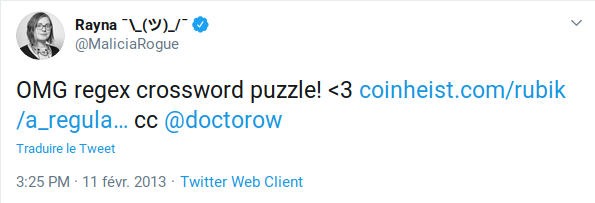
L'une des grilles hexagonales qui m'a le plus plu jusqu'ici vient d'un tweet que, jadis, Rayna/@maliciarogue avait posté : c'était une grille de crossregex, qui proposait de construire des expressions régulières sous forme de mots-croisés. JOIE. Rapidement, je remarquais que j'avais de sérieux progrès à faire niveau regex, mais cette fois-ci, comme ça servait pour la manipulation de corpus numériques aussi, j'ai fourni le travail nécessaire pour comprendre les expressions qui me faisaient défaut et ainsi terminer la grille proprement. Je découvrais alors qu'il existait d'autres grilles de crossregex accessibles à tous niveaux, et que c'était même un bon moyen pour enseigner les regex.

Pourtant, si je sentais que ça me profitait de passer du temps à m'occuper de ces puzzles, si je voyais très bien que j'apprenais des mots inconnus, ou retenait le principe des quantificateurs dans les expressions régulières, je n'ai jamais eu la sensation qu'en jouant à ces jeux j'étais en train de m'exercer à une logique propre à l'écriture scientifique elle-même. Cette sensation, je ne l'ai perçue qu'au contact des puzzles de Simon Tatham, au moment où je refaisais une dernière fois un plan de thèse avant de me lancer dans l'écriture (oui, j'en ai fait un certain nombre, de plans de thèses).

Les puzzles de S. Tatham et l'exercice de rédaction

Simon Tatham, déjà, n'a pas inventé les puzzles qu'on lui attribue, mais il les a codés afin de les rendre accessibles sur des ordinateurs personnels. Parmi eux on compte un équivalent du mastermind (où l'on doit deviner les couleurs des pions cachés et préalablement sélectionnés par l'adversaire), un autre du sudoku, un autre encore du célèbre démineur de windows, etc. Et puis des fois, ce n'est même pas lui qui les a codés, mais d'autres personnes qui se sont jointes en cours de route à son initiative. Surtout, il a eu la fine idée d'accompagner le code des puzzles d'une licence libre. Dès lors, les puzzles ont été intégrés aux principales distributions linux, à commencer par Debian, et sont aujourd'hui téléchargeables pour les tablettes et téléphones fonctionnant sous android et dérivés d'android dégooglisés tels que lineageOS.

Tatham maintient un site web sur lequel les puzzles sont listés et où l'histoire de leur collection est développée plus précisément. Il en existe environ une quarantaine. Concrètement, les puzzles ne sont pas les plus beaux du monde, en réalité, ils sont même plutôt moches. Cependant, ils sont visuellement sobres, sans publicité (!!!), fonctionnels et stables sur tous les systèmes (*nix, windows, Mac, java, etc.). Et, comparés à quantité d'applis de puzzles qui servent essentiellement à tracer les autres usages des téléphones mobiles ou fourguer de la publicité quand on joue dans le bus, les puzzles de Tatham sont certes une source de plaisir immense, mais aussi n'entraînent aucun désagrément capitaliste.

Tous les puzzles de cette collection ne m'ont pas intéressés, même s'il en existe de vraiment biens dont je ne vais pas parler ici (notamment pattern , unruly , map . Ceux qui comptent pour ce post sont ceux qui m'ont permis principalement de comprendre comment procéder pour organiser le plan d'un très gros texte et comment procéder pour se représenter les étapes et le rythme d'un texte qui ne peut jamais être vraiment envisagé de façon globale avant d'être terminé. D'autres fois, les puzzles m'ont fourni le moyen de schématiser quelque chose que je n'arrivais pas à formuler autrement et pour lequel je ne trouvais aucune inspiration dans la littérature scientifique dont je disposais.

En somme, les puzzles de Tatham ont permis que le travail de thèse, que je voyais avant tout comme un travail d'enquête, avec ses choix théoriques ou méthodologiques, ses stratégies et ses démonstrations, cesse d'être une sorte de tempête intellectuelle permanente et se transforme en un objet écrit. Ils m'ont fait accepter de ne produire qu'un objet écrit. En fait, les puzzles m'ont permit de pratiquer une métaphore de la rédaction, et de la pratiquer sans devoir penser au contenu de la rédaction, seulement à son processus et sa structure. Ceci implique d'accepter de réduire ce qui anime les pensées pour pouvoir à terme les matérialiser. Et, si je suis convaincu que des personnes ayant une plume déjà bien entraînée s'en sortent sans souci, dans mon cas, il a fallu penser la rédaction du manuscrit comme un puzzle pour parvenir à l'amorcer puis l'achever.

Petites mécaniques de linéarisation et d'ordonnancement

Cette puzzlisation de la rédaction de thèse ne s'est pas engagée à la suite d'une décision de ma part, c'est plutôt par fréquentation concomitante des puzzles et de l'éditeur de texte que la relation pratique entre les deux m'est apparue petit à petit : je percevais en écrivant que j'activais parfois le même mécanisme qui m'avait servi peu de temps auparavant à résoudre tel ou tel puzzle. Une chose drôle à ce sujet, c'est qu'une fois l'étape du plan très détaillé passée, j'ai immédiatement éprouvé un dégoût pour le puzzle qui m'avait mis sur la voie de l'écriture du plan, et n'y suit d'ailleurs revenu qu'une fois la thèse soutenue... Aussi vite que j'abandonnais un type de puzzle, j'en trouvais un autre qui me plaisait bien mieux et finissait par s'accorder pas mal à ce que je devais réaliser ensuite pour la rédaction. Ce fut le cas notamment en passant de signpost à unequal et towers.

Le premier puzzle, le plus important pour moi, c'est signpost . Les autres ont eu un rôle plus ponctuel et je ne vais pas les présenter de manière aussi développée ici. J'aborderai seulement unequal et towers pour pointer la complémentarité qu'ils entretiennent avec signpost dans la compréhension des logiques linéaires d'assemblages d'éléments dispersés.

Signpost et l'élaboration d'un plan détaillé

Signpost m'a offert les moyens d'envisager de façon pratique la réalisation d'un plan détaillé dans lequel il s'agit d'aligner des choses qui ont émergé dans les années précédentes sous des formes textuelles différentes (articles, slides, brouillons, etc.), à des moments différents pour des raisons différentes (séminaires, notes, fiches de lectures, etc.), rien de moins linéaire que les éléments d'une thèse en SHS avant rédaction.

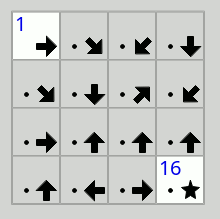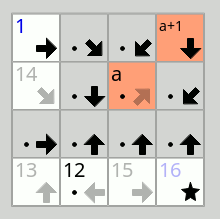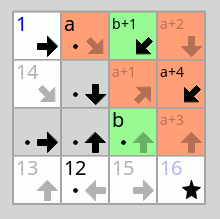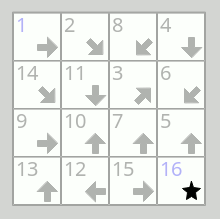
Pour présenter rapidement la règle du jeu¹, il s'agit donc d'ordonner l'ensemble des cases disponibles dans une grille, sachant que les cases sont soit marquées d'une flèche pointant en direction de la case qui les suivra (sans la désigner explicitement, le quadrillage formant donc un graphe de vecteurs dirigés), soit marquées d'une flèche ET d'un chiffre, les situant immédiatement sur la ligne globale qu'il s'agit de composer au fur et à mesure. On commence généralement en reliant les cases chiffrées qui se suivent et les cases uniquement fléchées qui pointent vers une seule case (les cases situées au bord de la grille). À partir de là, différentes stratégies sont possibles, mais le chemin sera globalement le même pour tout le monde avant de terminer le puzzle.

Dans signpost, le travail se fait toujours localement, et on commence par de toutes petites séquences au sein d'un réseau en apparence inextricable. Dans une rédaction de thèse, on commence aussi par de petites séquences, et ce même si l'on a sûrement de grandes ambitions au départ ou que l'on a déjà publié des articles (c'est-à-dire déjà formulé certains des éléments à travailler). On démarre donc avec quelques paragraphes, des blocs d'idées, des descriptions, des synthèses d'ouvrages, etc., des éléments qui sont extraits de manière en apparence chaotique de sa *pensée* sur le sujet, de l'enquête (pas toujours bien terminée encore, parfois). Il faut faire sobre, synthétique, résumer, annoncer, il n'est plus possible de copier-coller 15 pages de description et de considérer que ça ira.

Certaines zones de la grille de signpost resteront floues très longtemps avant de prendre sens, c'est-à-dire qu'on ajoute des séquences au fur-et-à-mesure qu'on découvre des éléments dans le réseau de départ. Parce que, finalement, signpost n'est pas de ces quadrillages qu'il faut remplir. Le quadrillage est toujours comme déjà plein, il doit plutôt être dévoilé, exhumé comme un vestige sur un champ de fouilles archéologiques (un peu comme le raconte Gérard Fromanger qui explique que la toile du peintre est déjà noire d'images, qu'il faut pouvoir sélectionner dedans pour la simplifier, éliminer des formes parasites, avant de la faire aboutir... cf.Dautrey, Jehanne. « Peindre sous l'image : Gérard Fromanger, un usage contemporain de la perspective », Communications, vol. 85, no. 2, 2009, pp. 103-115.).

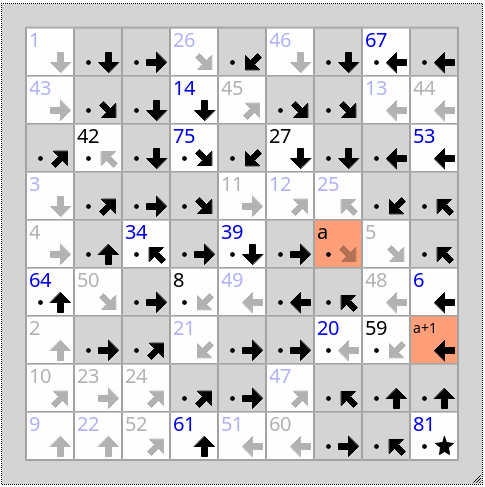
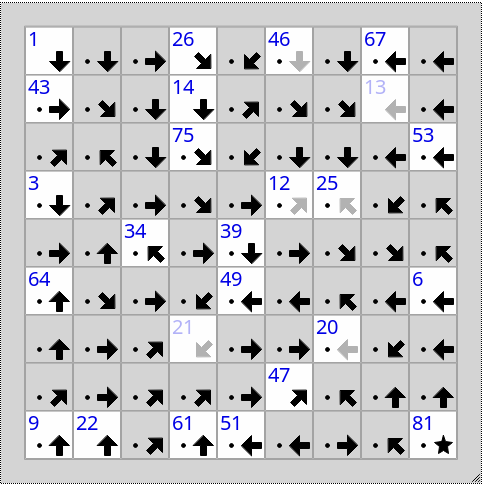
Certaines de ces séquences vont s'agencer ensuite en de plus grosses séquences, mais pas toujours suivant les mêmes critères. Dans signpost, soit on ordonne deux cases parce qu'une flèche et le contexte indique qu'elles se suivent, sans savoir où exactement elles prendront place dans la ligne complète, soit on localise deux cases comme voisines parce qu'elles contiennent des chiffres qui se suivent en plus des flèches, ce qui les ordonne de fait. On sait souvent que certaines idées doivent être présentées au lectorat avant d'autres pour que le raisonnement soit limpide, cela ne signifie pas toujours que l'une et l'autre des idées ordonnées se trouveront dans le même chapitre, ni dans quel chapitre elles apparaîtront au final. Mais, au moins, on connait leur ordre. Et puis il y a les idées que l'on sait dès le départ qu'elles sont préliminaires ou finales, chapitre 1 ou chapitre N, reste à y raccrocher toutes les autres, et il peu y en avoir beaucoup.

Ce que l'on constate aussi dans cette grille, c'est que certains éléments restent flous jusque tard dans le travail, et que finalement, ce n'est pas grave, on ne peut pas tout faire en même temps. avoir ce principe à l'esprit n'est pas si facile tant que l'on n'en a pas encore constaté les effets miraculeux. Lorsque je les accompagnais dans la construction de leur plan détaillé, j'ai vu nombre de masterant·es et de doctorant·es être envahi·es par un désespoir terrible de devoir abandonner en fin de journée un plan "pas terminé", de devoir constater que les idées n'étaient pas venues aisément s'emboîter dans des chapitres accueillants. Bien entendu, un plan ne se fait pas en 30 minutes, et sa construction va passer par plusieurs étapes de refonte parfois complète (ce qui n'arrive pas dans signpost en revanche...). Trouver ce qui va avant et ce qui va après n'est pas compliqué à se représenter. Néanmoins, si signpost ordonne globalement à partir d'une suite de chiffres, dans la rédaction il faut construire soi-même, en parallèle de la construction et de l'ordonnancement des petites séquences, le critère final de linéarisation, le fil rouge narratif du plan détaillé, qui va trouver une cohérence intrinsèque et contenir en les agençant toutes les petites séquences identifiées auparavant.

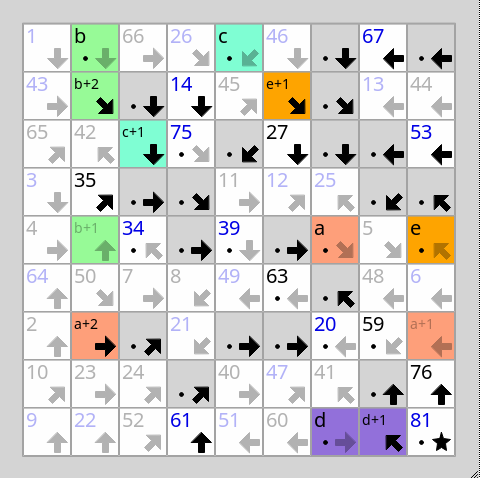
Dans signpost il est aisé et instantané de passer de l'ordre indiqué par la direction des flèches à l'ordre indiqué par la suite des chiffres qui se complètent. Pour la rédaction, l'exercice est un brin plus ardu, dans la mesure où le plan va se structurer de manière plus subtile qu'une simple suite de chiffres. On n'ordonne jamais seulement localement, par contiguïté, il faut un principe ordonnateur global, c'est là que le plan général, les grandes lignes de la thèse qui tiennent en deux ou trois pages (qui grossira par la suite), intervient au même titre que l'ordre des nombres de 1 à 100 (si on joue à signpost avec une grille de 10 carreaux de côté).

Seulement, dans le cas du plan, le passage d'un critère servant à agencer une petite séquence (par exemple, une démonstration depuis des éléments empiriques) à un autre critère agençant une autre petite séquence (par exemple, la critique d'un·e auteur·rice) n'est pas aussi évident : une observation faite sur le terrain, même déjà formulée au sein d'une analyse partielle, a de grandes chances de devoir être encore transformée pour s'articuler avec la critique de connaissances déjà établies auparavant par d'autres personnes. Sauf que, petit à petit, on avance, et même lorsqu'il reste du flou, il y a aussi des zones qui deviennent plus stables et prêtes à rédiger. Alors, comment termine-t-on ? Et bien, si terminer une grille de signpost est en général assez facile, ce puzzle n'aide pas pour autant à saisir comment terminer un plan détaillé...

Unequal et towers pour un éclairage complémentaire

En réalité, il manque quelque chose à signpost que l'on trouve dans d'autres puzzles, unequal et towers notamment...

Le principe de unequal est à la fois plus simple et plus compliqué que celui de signpost : on a deux critères d'ordonnancement un numérique et un fléché, mais ils ne fonctionnent pas comme dans signpost : l'ordonnancement de nombres suit les lignes et les colonnes plutôt qu'il ne s'applique de manière linéaire à l'ensemble des cases de la grille. De plus, les flèches ne sont plus systématiquement présentes et n'indiquent plus une direction dans l'espace de la grille, mais un rapport d'infériorité/supériorité sans contiguïté obligatoire entre les chiffres qu'il faudra deviner pour deux cases voisines. Passé un certain niveau de difficulté, une grille initiale de unequal est, au contraire de celle de signpost, pratiquement vide, à l'exception de quelques flèches ici ou là. Ce puzzle engage finalement un raisonnement très différent du précédent.

Dans le cas de signpost, l'augmentation de la taille de la grille ne demande pas d'efforts importants pour terminer le puzzle, seulement de la patience et de la constance. En gros, on pourrait dire que les manière de le résoudre sont assez facilement 'scalables', c'est-à-dire que le changement d'échelle de la grille ne pose pas de difficultés supplémentaires. Il n'en va pas exactement de même pour unequal, et la difficulté qui s'ajoute avec l'augmentation de la taille de la grille est très intéressante pour métaphoriser la rédaction d'un plan. En effet, même si je suis bien incapable d'expliquer pourquoi (j'ai la flemme de chercher, pour être honnête...), l'augmentation de la taille de la grille participe largement d'une complexification des déductions à opérer, et il devient essentiel de noter (le puzzle le permet techniquement, bien entendu) des déductions intermédiaires, un peu comme pour les sudokus à partir d'un certain niveau. Le niveau augmente et demande alors de nouvelles manières d'avancer.

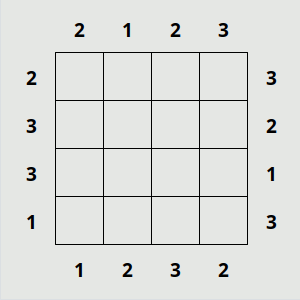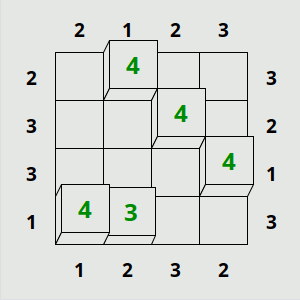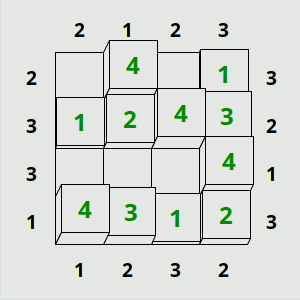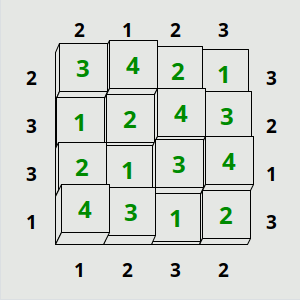
Towers demande un peu le même type de raisonnement que unequal, ils sont relativement cousins. la principale différence réside dans le fait que, contrairement à signpost et unequal dans lesquels les indices concernent principalement les rapports entre deux cases à chaque fois, towers fourni des indices uniquement pour des lignes ou des colonnes entières. Il faut dès lors croiser ces indices, plus rares au fur et à mesure que le niveau et la taille de la grille augmentent, afin d'en déduire la façon dont on va remplir les cases. L'objectif consiste à deviner combien de tours seront visibles sur la ligne depuis l'endroit où l'indice est écrit (les tours, ne sont que la représentation d'un chiffre, bien entendu). Le lien entre deux cases voisines n'est pas forcément spécifié de manière direct, mais il va être déduit, une fois de plus, du croisement d'informations présentes à d'autres endroits de la grille.

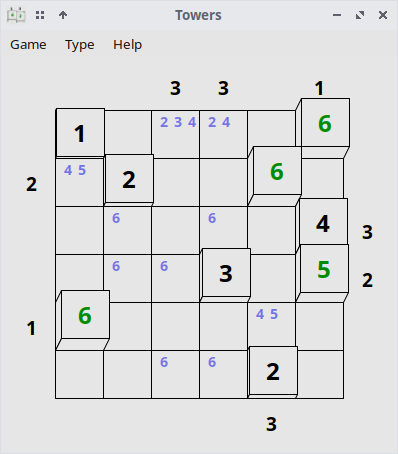
Comme dans unequal, il s'agit de travailler les "déductions certaines" à partir de déductions "intermédiaires". D'abord, il faut bien saisir cette histoire de déductions intermédiaires : les chiffres que l'on peut accumuler en tout petit dans chaque case, alors qu'il n'existe qu'un seul résultat valable, ne sont pas des hypothèses qui demanderaient démonstration, mais seulement des formes temporairement inabouties de la déduction. Et c'est à partir de la vision d'ensemble de ces déductions intermédiaires, sur une zone de la grille au moins, que l'on va pouvoir déduire définitivement le résultat d'autres cases, parfois à l'autre bout de la grille. Il faut donc avancer un peu "dans le vide", bien que ce soit la pire chose à demander à quelqu'un·e déjà complètement flippé·e de se lancer dans la rédaction. Appréhender cet "élan" en apparence complètement kamikaze à l'échelle d'un puzzle permet de dédramatiser l'affaire, et de comprendre en quoi l'avancée pas à pas et sans vision complète de l'ensemble va justement permettre de construire l'ensemble en question, en l'occurrence, le plan détaillé qui pourra, dès lors, servir de guide à la rédaction de chacune des pages à venir.